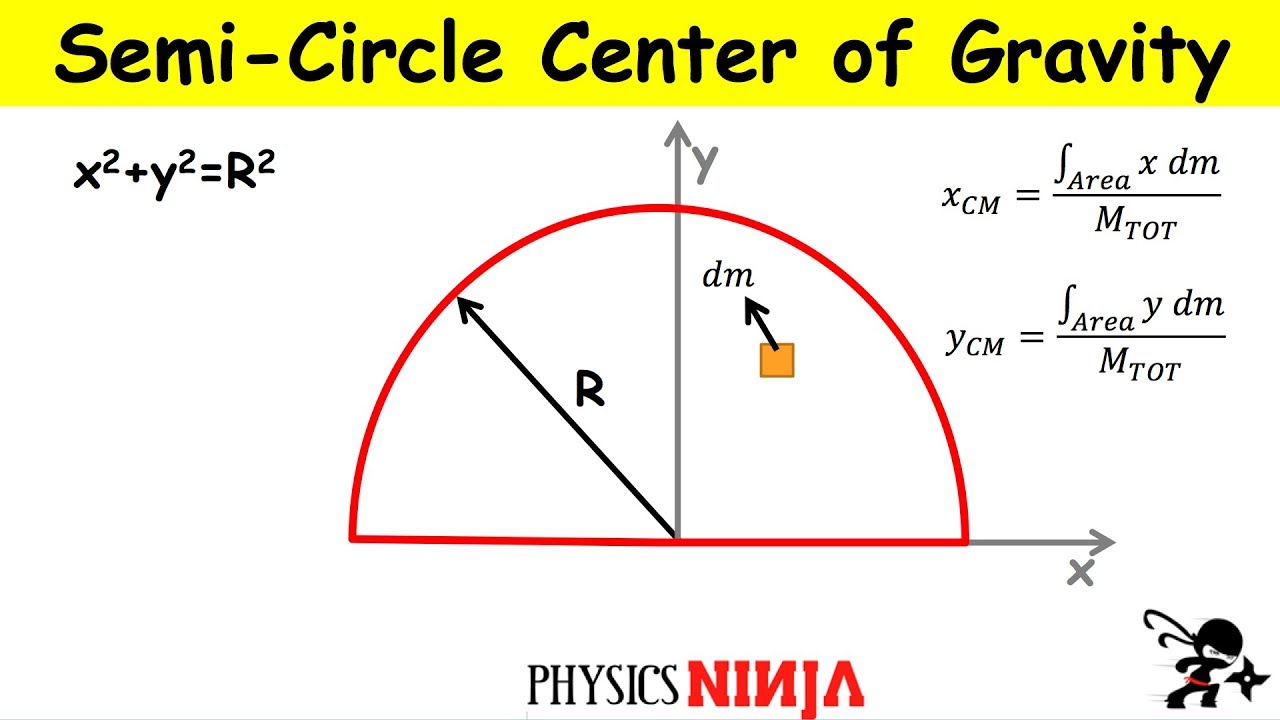
Semicircle Center Of Mass. We can model a semicircle as a stack of infinitesimally thin strips. It is found by using a string vertically suspended between two points inside the figure.
A piece of wire 23 m long is cut into two pieces. Informally, it is the average of all points of x {\displaystyle x}. By the pappus centroid theorem, 2 π d ⋅ π 2 r 2 = 4 π 3 r 3, hence d = 4 r 3 π.
The Centroid Is The Location That We Can Model The Shape As If The Entire Weight Acts Through This Point.
The centre of mass satisfies. We have and since the semicircle is uniform we have where is the area of the semicircle, ie. A semicircular arc has its center of mass at ( 0, 2r/pi).
A Particle Of Mass M Is Placed At The Center Of The Circle.
Determine the coordinates of its center of mass with respect to an origin of coordinates at the center of the full” circle. Find the gravitational attraction on the particle due to the wire. 1.9k views · answer requested by
For Instance, The Centroid Of A Circle And A Rectangle Is At The Middle.
Calculate the magnitude of the force on a point of mass m = 74 kg placed at the center of the semicircle, as shown in the figure. A uniform rod of mass m = 326 kg is in the shape of a semicircle of radius r = 6 m. If the object has a uniform density, then the centroid is also the center of mass, which is the point at which the object will balance with just as much mass on all sides.
A Semicircular Wire Has A Length L And Mass M.
Hence, the center of mass of a semi circular ring lies on the vertical passing through its center of curvature at a distance of $\dfrac{2r}{\pi }$from the center of curvature. We know that the centre of mass lies on the red line, since this is a line of symmetry of the object. We know that moment of inertia along the centre of the semicircle is m r 2 2 and the distance from the centre to the point of centre of mass is 4 r 3 π.
This Page References The Formulas For Finding The Centroid Of Several Common 2D Shapes.
(ii) a uniform thin wire is bent into a semicircle of radius r. To see why, look at the definition of. In the case of a one dimensional object, the center of mass r → cm, if given by.
Related Posts
- Byu Testing Center Hours Finals WeekByu Testing Center Hours Finals Week. All byu online exams are offered through the online exam proctoring service examity. (final exams will be moved ...
- Molar Mass Of Aucl3Molar Mass Of Aucl3. Explanation of how to find the molar mass of aucl3: 2 rows molar mass, molecular weight and elemental composition calculator ent ...
- Molar Mass Of MgohMolar Mass Of Mgoh. What is the solubility of mg oh 2 in a ph 12.0 solution? The molar mass is the mass of a given chemical element or chemical compo ...
- Cuno3 Molar MassCuno3 Molar Mass. Cuno3 molar mass = 63.5 + 14 + 3(16) = 125.5 grams/mol 8.22 g /125.5 g/mol =.0655 mols of the stuff.0655 mols/x liters =.59 mols/1 ...
- Molar Mass Of Leadii NitrateMolar Mass Of Leadii Nitrate. Its melting point is 270 ̊c (518 ̊f), density 4.53 g/cm3. What is the molar mass of pb no3 4?Molar Mass / Molecular Wei ...
- Molecular Mass Of OctaneMolecular Mass Of Octane. The molecular mass of octane is 114.22 g/mol. Interpreting the fragmentation pattern of the mass spectrum of octane [m] + i ...
- K2So4 Molar MassK2So4 Molar Mass. Convert grams k2so4 to moles or moles k2so4 to grams. ¿es esta web útil para ti?K2so4 Molar Mass from divinewsmedia.comTo find the ...
